Lógica binaria
La lógica binaria trabaja con variables binarias y operaciones lógicas. Así, las variables sólo tomarán dos valores discretos: V (verdadero) y F (falso); aunque también se pueden denotar como sí y no, ó 1 y 0 respectivamente.
Principio de dualidad
Todas las expresiones booleanas permanecen válidas si se intercambian los operadores '+' y '·', y los elementos '0' y '1'.
Así para obtener una expresión algebraica dual, se intercambian los operadores AND y OR y se reemplazan unos por ceros y viceversa.
Tablas de verdad de las operaciones binarias fundamentales
AND
Resumiendo, el resultado siempre dará 0 a menos que ambas variables valgan 1. (Equivale a la multiplicación)
OR
Resumiendo, el resultado arrojado será siempre 1 si al menos una de las variables tiene por valor 1.
NOT
El not es una inversión del valor como se ve. (Equivale a restar el valor inicial de 1)
Siguiendo el Álgebra de Boole se pueden combinar estas operaciones empleando varias variables y obteniendo resultados más complejos. A continuación una tabla de verdad de una operación lógica compuesta.
Ejemplo:
A · (B + C) = A · (B + C)
A B C Resultado
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
Axiomas [editar]
Las propiedades definen reglas precisas para transformar unas expresiones en otras equivalentes. Los axiomas son propiedades primitivas.
Propiedad conmutativa (el resultado no depende del orden)
Propiedad asociativa (el resultado no depende de el modo de asociación)
Propiedad distributiva (una operación se distribuye en una asociación)
Otras propiedades
Leyes de Morgan
Operadores no fundamentales XOR, XNOR e IMPLIES
Los operadores no fundamentales pueden expresarse a partir de los operadores fundamentales
- XOR:
XOR se conoce como OR exclusiva
- XNOR:
XNOR equivale a sí-y-sólo-si
- IMPLIES:
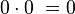



















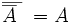








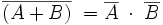
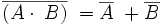














No hay comentarios:
Publicar un comentario